An nth order moment of x is defined as:
An nth order central moment is defined as:
In terms of density function f(x) moments can be expressed as:
Sharpe Ratio:
Sharpe Ratio is a popular measure of risk adjusted rewards. The rewards are considered to be the first moment of excess returns(x-MAR). Here x is the series of returns and MAR is the minimum acceptable return. The square root of second central moment of returns is considered as the risk. Its popularity can be attributed to the simplicity with which it can be calculated.
But one must be aware that these implicit assumptions about the nature of risk and rewards can be misleading. Sharpe ratio treats volatility on either side of MAR equally. This means that for a uniformly distributed return series with mean of 10%; a return of 110% is as worse as a return of -90%!!! Simply put volatility is a poor measure of risk. On similar lines Sharpe, considers any returns below the MAR as rewards.
Upside potential ratio:
Upside potential ratio helps us to eliminate both these concerns with the use of partial moments. An nth order partial moment is a one sided moments above/below the threshold. An nth order lower partial moment (lpm) for a threshold t is defined as:
Similarly an nth order upper partial moment (upm) is defined as:
Upside potential ratio is the ratio of first order upper partial moment to that of square root of second order lower partial moment both about MAR. Hence essentially it’s a measure of upside performance with respect to downside risk.
Comparison:
Let us consider two series A and B both identical in all respects except that B has some positive skew. Clearly B would be preferred over A as returns of a trading strategy.
Series
|
Mean
|
Variance
|
Skew
|
MAR
|
Sharpe Ratio
|
UPR
|
A
|
1.4973
|
0.9966
|
-0.0108
|
0
|
1.4999
|
10.0886
|
B
|
1.4940
|
0.9992
|
0.4088
|
0
|
1.4946
|
19.0381
|
The Sharpe ratio of A and B are essentially the same but there is a significant difference in the Upside potential ratio thus giving us better resolution of the returns. An important thing to note here is that though Upside potential ratio does not take higher moments into consideration per say, the asymmetry caused by skew has been accounted by the partial moments.
A practical use of Upside potential ratio is in
strategy selection. Typically, a mean reverting (MR) strategy has a much higher
Sharpe ratio when compared with a momentum (MM) strategy. But MR strategies are
more exposed to tail risk due to absence of stop loss. Hence in terms of moments, for the same mean
returns:
1) Volatility of MM strategy > Volatility
of MR strategy
2) Skew for MM strategy> Skew of MR
strategy
This means, Sharpe ratio gives undue advantage
to MR strategies. With the use of Upside potential ratio this bias can be minimized
and a better strategy level diversification can be achieved.




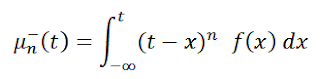



No comments:
Post a Comment