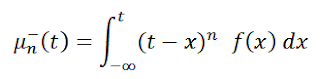Factor analysis is a multivariate statistical method aimed
at data reduction and summarization. It can be used to describe the covariance relationships among many variables in terms of a few hidden underlying factors.
Suppose we have a number of correlated variables. Using the
correlation matrix, we can group these variables such that the variables within
a particular group are highly correlated among themselves, but have relatively
small correlations with variables in other groups. This means that each group
of variables represents a single underlying construct or factor. These factors
can have a fundamental meaning attached to them.
Use of Factor Analysis in trading
Factor analysis are used in trading and portfolio management for various reasons:
- It is used to identify hidden factors/trends which drive the asset returns. These factors will typically have a fundamental meaning(like sector/style) attached to them.
- It is used to classify assets into groups based on their returns. There is a gamut of trading strategies(like basket long short) that can be implemented within each of these groups.
- It gives a clear picture of the major source of the portfolio risk. These risks can be either systematic (common variance) or unsystematic (specific variance) and hence handled accordingly.
Classification of LIX15 stocks
Looking at the above stock list we can say that these factors approximately represent different sectorial themes. The first factor is populated with financial services stocks. The second factor has a large number of metal stocks.
There are some stocks in each factor that do not concur with the corresponding fundamental interpretation. This would primarily be sample bias. Another reason could be that these fundamental factors indirectly affect the returns of the corresponding stocks. Also there are some stocks which do not have significant loading on any of the factors. MCDOWELL-N, TATAMOTORS and CAIRN are some of these stocks. These stocks do not fall in either of the sector and hence have remained unclassified.
LIX15 is an
Indian equity market index that consists of 15 highly liquid stocks traded on
National stock exchange. Factor
analysis is performed on the returns of these 15 stocks to identify any hidden
trends. The observations matrix consists of normalized daily returns of these
15 stocks sampled from February to November 2013. A two factor model is chosen
to decompose the data. The factor loadings are determined using maximum
likelihood estimation method. It is seen that these factors accounts for about
60 % of the total variance. Now VARIMAX rotation is performed to group stocks
based on their loadings. The aim of this rotation is to achieve simple
structures which will possibly have a fundamental reasoning behind them. The following is the table of top 6 stocks with highest loading on each factor:
Factor I
|
Factor II
|
AXISBANK
|
TATASTEEL
|
YESBANK
|
HINDALCO
|
SBIN
|
JSWSTEEL
|
IDFC
|
JPASSOCIAT
|
BANKBARODA
|
RCOM
|
MARUTI
|
JINDALSTEL
|
Looking at the above stock list we can say that these factors approximately represent different sectorial themes. The first factor is populated with financial services stocks. The second factor has a large number of metal stocks.
Fundamental theme
|
|
Factor 1
|
Financial services stocks
|
Factor 2
|
Metal stocks
|
There are some stocks in each factor that do not concur with the corresponding fundamental interpretation. This would primarily be sample bias. Another reason could be that these fundamental factors indirectly affect the returns of the corresponding stocks. Also there are some stocks which do not have significant loading on any of the factors. MCDOWELL-N, TATAMOTORS and CAIRN are some of these stocks. These stocks do not fall in either of the sector and hence have remained unclassified.
Classification of BANKNIFTY stocks
BANKNIFTY is the primary banking sector index of India. Similar to the LIX15 analysis, a two factor decomposition
of the twelve BANKNIFTY constituents is performed. About 75% of the total
variance is explained by these two factors. Following is the table of top 6
stocks with the highest loading each factor.
Factor I
|
Factor II
|
AXISBANK
|
CANBK
|
ICICIBANK
|
BANKINDIA
|
HDFCBANK
|
UNIONBANK
|
INDUSINDBK
|
BANKBARODA
|
YESBANK
|
PNB
|
KOTAKBANK
|
SBIN
|
It is clear that the Factor 1 corresponds to private sector
banks and Factor 2 corresponds to public sector banks. Hence within the banking
sector the most dominant segregation is along the public verses private lines.
Fundamental theme
|
|
Factor 1
|
Private sector banks
|
Factor 2
|
Public sector banks
|
Conclusion:
The prices of stocks
are typically correlated. Using factor analysis, we can group the variability in
the stock market into categories. We can now view fluctuations in the stock
market based on groups rather than the individual stocks. Using factor analysis
we have been able to conclude that among the LIX15 constituents the major classification is on the sectorial lines. Also among the BANKNIFTY constituents the classification lies along the public vs private ownership lines.