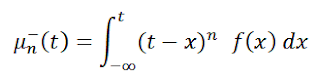Trade cost is a tricky subject. It has significant impact on the strategy performance and yet it is one of the least understood subjects. It is typically assumed away in literature. Both underestimation and overestimation of trade cost has detrimental effects. Underestimation of cost can lead to higher churning and thus hurt us in multiple ways. Over estimation of trade cost can force one to trade too slowly and hence can lead to significant market risk.
Components of trade
cost:
- Direct costs such as brokerage, taxes etc. This component is easy to measure.
- Indirect costs such as market impact and opportunity cost. Market impact is the cost incurred from the market in order to enter or exit a position. This component is hard to measure
Why bother with an accurate
trade cost models?
- Trading cost can have a very significant impact on returns of strategies with high churning ratio. This mean a trading cost model is imperative if you play in the domain of statistical arbitrage or HFT.
- An accurate impact cost model can help one alter the trading strategy to achieve higher returns. Given a generic trading idea, should I trade on large cap or on small cap stock universe? The answer to this question would not only depend on gross returns in both these universes but also on the incurred impact cost (for a given trade size).
- It also helps one determine the maximum capacity of a particular fund. Beyond a certain size, the fund returns might fall down to less than acceptable levels
- It can help us design and evaluate order execution algorithms.
Forces at play:
Market impact cost is the difference between the pre trade paper price (LTP or mid price as the modeling may be) and the realized trade price. The characteristics of the underlying asset (liquidity, volatility, resiliency etc) and our order (size, execution strategy etc) both determine the impact cost. The following observable variables play a major role in determining the impact cost:
- Relative order size (ROS): It is the ratio of our order size to the total traded quantity in the period. As it is hard to figure out how much quantity is going to be traded in the future, average of last n day trade volume can be used as a proxy. Impact increases with trade size either linearly or at a decreasing rate.
- Bid/Ask spread (S): It is the normalized spread of the order book. Impact increases linearly with the spread.
- Volatility (V): More volatile assets tend to have higher impact cost (because of price chase and premature order fills). Impact increases with volatility at a decreasing rate.
- Trading rate: If trades follow one another in quick succession, there will be an increased market impact (as each trade will move the price from where the previous trade left it). This happens because the order book has no time to recover from the impact of previous trades.
- Trend cost: Selling a falling stock will have much higher impact cost than buying it. This implies that the delay between trade signal generation and trade execution will affect short term momentum strategies a lot more than their counterpart.
A calibrated impact cost model would look something like
this:
Best way to get an accurate picture of impact cost is to
collect the impact data on a trade by trade basis. And then use this data to
calibrate the chosen model. There is an easier way to get a rough estimate of
the incurred impact cost. By comparing the live trade returns with the back
test returns (rerun the back test model during the live period) approximate
values can be arrived at. Here one would be assuming that the real live effects
not taken into account while back testing (stock alterations, inability to
trade on closing price etc) average out to zero.
A word of caution, these impact cost estimates will work
only in usual circumstances. For very big orders or extreme level of market
volatility these models can give unrealistic estimates of market impact. So with the calibrated model one must also
specify the boundary conditions.